
Andrew Stone, Bitcoin Unlimited, g.andrew.stone@gmail.com
Blockchain consensus algorithms that use automatic trailing checkpoints (finalization) and additional proof-of-work requirements (parking) in their consensus algorithms are susceptible to persistent forks. The probability of attacker success is analyzed and compared to other algorithms. While autofinalization is shown to be a tradeoff that makes doublespend reorganization attacks harder at the expense of allowing persistent forks, parking makes creating persistent forks much easier, and only reduces the likelihood of reorganization of pre-finalized blocks.
The consensus achieved by the parking and auto-finalization technologies in Bitcoin Cash prevents intentional chain reorganization. But they are inconsistent with consensus theory and that strongly implies that these technologies are not innovations in consensus but rather trade correctness for convenience. This paper provides an analysis that describes specific attacks against auto-finalization and parking and shows the cost and likelihood that a malicious miner could successfully execute them.
Persistent fork in this paper means a failure of the consensus algorithm to achieve consensus, requiring an extra-algorithmic correction. In practice, this would mean a fork of the blockchain that first requires human consensus to pick one of the two forks, and then human intervention at every node that followed the wrong fork to manually force a blockchain reorganization.
Finalization is a technique to create non-persistent blockchain checkpoints. All forks that do not contain the finalized block are marked invalid persistently. Full nodes can be directed to consider one particular block, F, “final”. F is stored in RAM and any blocks that are not on F’s chain are marked as invalid. This is not quite a checkpoint for two reasons:
These differences are noted here for precision but may simply be an implementation convenience.
Auto-finalization is a process where the main chain block that is at the auto-finalization depth (which is 10 on BCH) is marked as the “final” block.
Parking is a modification to the rule that determines the main chain proposed by Satoshi1 “Nodes always consider the longest chain to be the correct one and will keep working on extending it.” The parking technique observes that a full node that is not in “initial block download” mode has a fork that it currently sees as the main chain (M), and a candidate fork ( C ) that it is considering switching to. A full node that implements parking will not switch to C unless it exceeds the work in M by an amount that varies depending on the length of the fork M, called extra parking work (EPW):
forkBlock=LastCommonBlock(M,C)(1)
mainForkLength=Height(M)−Height(forkBlock))(2)
EPW=⎩⎪⎪⎨⎪⎪⎧2Work(M)−Work(forkBlock) if mainForkLength is 12Work(M−1)−Work(forkBlock) if mainForkLength is 2 or 3Work(M)−Work(forkBlock) otherwise(3)
If we make the simplifying “steady state mining” assumption that each block requires approximately the same amount of work w, then this equation simplifies to:
EPW=⎩⎪⎪⎨⎪⎪⎧2w if mainForkLength is 1 or 2w if mainForkLength is 3w∗mainForkLength otherwise(4)
The auto-finalization and parking logic was added to the Bitcoin ABC client in response to the Bitcoin Cash/Bitcoin SV fork. At that time, there was fear that a short-term economically irrational actor would continually reorganize the Bitcoin Cash fork with empty blocks (or execute other attacks). Doing so would block all transactions from confirming on-chain, encouraging abandonment of the fork. By finalizing blocks 10 deep, no deeper reorganization can occur. But it was observed that this is not good enough since an attacker could simply release its reorganizations every 8 or 9 blocks, although it does prevent double spend attacks (since exchanges would not release funds until finalization occurred). Parking was proposed to discourage this activity, since an attacker would have to produce twice as much work to cause a reorganization, except for the first 3 blocks. One might expect that an attacker simply reorganize every 2 or 3 blocks, since the parking algorithm requires much less extra work for forks of those lengths. However even with majority hash power, there is a probability that the attacker will fail to create the longest chain, and this probability increases as the depth decreases. So the honest minority would be able to get blocks confirmed and given BCH’s utilization these few blocks could confirm all existing transactions. For example, if the honest miners have only 20% of the hash power, they will win a 3 block race 5.2% of the time but a 9 block race only 0.1% of the time1.
No such attack materialized.
The well known double spend attack has been used to steal millions of dollars7,8. It actually comprises two components: the actual double spend transaction, and a blockchain reorganization that occurs because a privately generated fork is released. A persistent fork can be used in place of the release of the privately generated fork in a double spend attack because eventually people need to “heal” the fork by choosing one of the chains as the “main” chain and manually reorganize the nodes on the other chain. Although there is some uncertainty as to which chain people would choose, an attacker could run double spends on both forks to different services, or in other ways make one chain more palatable than the other. For example, they could organize things so choosing the “fraud” chain awards all mining fees to the attacker, or confirm no other transactions, providing the general public an opportunity to run double spends against old, rewound transactions.
But a simpler attack might be to short the cryptocurrency on multiple exchanges and trigger persistent forks since the disruption is likely to cause significant loss of confidence.
For completeness Eclipse/Partition Attacks and node synchronization failures are mentioned next. However the main attack presented in this paper is the “fork matching” attack, described in section 3.
An eclipse or partition attack is an attack in which the target node or nodes cannot communicate outside of the eclipsed group, except via the attacker.
If an attacker can maintain an eclipse or partition for the auto-finalization depth number of blocks, the isolated nodes will persistently fork from the other nodes.
Auto-finalization therefore imports the networking architecture and its source code into the forking attack surface of the cryptocurrency, whereas it was previously only a problem for double spend attacks.
The effect of chain parking is that nodes do not immediately switch to the most-work chain. Instead they stick with the “current” chain. This “current” chain is the most-work chain in the set that the node’s connections are advertising. If this fork length is greater than the auto-finalization depth (10 blocks on BCH), it will be “finalized” and so persistently prevent switching.
There are two avenues of attack. In the first, the attacker creates a deep reorganization most-work chain. None of the existing nodes will switch to it due to their finalization rules. However, all new nodes in the system will synchronize to it (if visible during synchronization) and all SPV wallets will choose it.
This would be an expensive attack to maintain, but would force BCH developers to hard code a checkpoint into every full node and SPV wallet to rejects the attacker’s chain.
In the second attack, the attacker creates a lower-work fork 1 block longer than the auto-finalization depth anywhere (or in multiple places to gain multiple attempts) in the chain. It then attempts to push this fork into synchronizing nodes, causing finalization into this “dead-end”. If the synchronizing node is also successfully eclipse attacked, the attack will succeed since the node will not be aware of any greater work chain. Otherwise the success of the attack will fail given a careful implementation of synchronization that first validates the POW in most-work chain’s full header path, and second rejects any attempts to inject blocks into the node that are not on this path.
These problems were demonstrated during the BCHABC fork on Dec 1, 2020F3. [This section document was updated on Dec 2 to include this evidence]
This attack can still cause a persistent fork in a connected network – that is, no eclipse or partition attack is necessary. In summary, the attacker will cause a fork and maintain it for the auto-finalization depth number of blocks, whereupon the first forked blocks are finalized in every node, resulting in a persistent fork.
Let us first examine the attack against nodes that implement finalization but not parking.
To prepare for this attack, the attacker positions computing resources near full nodes associated with the services the attacker would like to fork. These full nodes can be identified reliably by techniques discovered in [3]. The attacker must be able to reliably be the node that provides the target full node new blocks. This is easy to verify before the attack begins, by determining whether the target node is requesting blocks from (issuing INV blocks to) an attack node. An attacker may also be able to employ protocol shortcuts (such as forwarding a block without header or INV, or forwarding the header and then the block without waiting for a GETDATA) to further increase its block propagation rate relative to other nodes, depending on the details of a node’s protocol implementation.
Note that if the attacker’s objective is general mayhem rather than forking specific target nodes and services, the attack is easier since it can be targeted towards N nodes but still succeed if some nontrivial number of nodes are forked.
In the first step the attacker triggers a fork F off of main chain M. This is accomplished by mining a block F0 and then waiting for another miner to mine a block M0. As soon as the attacker receives notification of the block M0, it forwards F0 instead, using any available protocol shortcuts. Based on the analysis done during setup, F0 will beat M0 to the target nodes.
The attacker now attempts to mine a number of blocks equal to the blockchain’s auto-finalization depth F1 to Ff. As main chain blocks are discovered by the rest of the network, the attacker propagates its blocks directly to its targets. This ensures that the target nodes see the attackers block first, but that (in general) the rest of the network does not.
A node does not switch from its current chain to an equal work chain, so as long as block propagation is controlled, the fork can be maintained.
There is a risk that the target nodes will propagate the fork to untargeted nodes, converting those nodes from M to F. There is also a risk that some of the target nodes will see the main chain block first, converting them from F to M. These risks may be acceptable depending on the attacker’s goals.
Once the fork has been maintained for the auto-finalization depth, the fork will become persistent and the attack can stop.
P1 “Attack Foiled”: The attacker must have produced as many or more blocks than the main chain miners every time the main chain miners produce a block, so that it can push the next block on F the moment a block on M is discovered. Analysis of the exact success probability of this is included below.
P2 “Attack Mistimed”: If the attacker presents Fn too early or late, it can cause nodes to move between forks F and M. Proper timing is experimentally easy to achieve on regtest. However, the only way to determine whether this applies to the mainnet is to try it. It turns out that it does not matter for “parking” nodes so the analysis of this problem stops here.
P3 “Attack Spoiled”: If the targeted nodes are miners, and they discover and propagate a block on F, the nodes mining M will switch to F, ending the attack. Note that since F is now the main chain, F has lost no money. Actually, this constitutes a selfish mining attack4 so F’s actions will increase its profitability on subsequent blocks by reducing difficulty. To put some numbers around this problem, the likelihood that a miner with hash power ‘p’ as a fraction of the total hash power does not produce a block in N nodes can be calculated. It is 1 minus likelihood that the rest of the hash power “wins” n times, or:
spoil probability=1−(1−p)n(5)
For example, targeting 5% of the hash power will be spoiled 40% of the time with an auto-finalization depth of 10. However, note that in cryptocurrencies like BCH, which command a small fraction of available hash power, it would not be difficult for a miner to direct a significant quantity of hash to both M and FF2, dramatically reducing the targeted hash power’s percentage.
P4 “ASERT interference”: Since ASERT recalculates difficulty for every block, is it near impossible to have the exact same POW on two forks? If so the fork will heal. Or will the “absolutely scheduled” nature of ASERT generally result in the same difficulty? It turns out that it does not matter for “parking” full nodes so the analysis of this problem stops here.
This attack differs from the traditional doublespend because the attacker must remain ahead of the main chain throughout the entire attack interval of auto-finalization depth (AFD) blocks.
Let:
T => mining interval in minutes/block, with 100% hash power (e.g. 10 minutes)
q => the attacker’s proportion of hash power
p = 1-q => honest miner’s proportion of hash power
So the honest miner’s mining interval (minutes/blocks)
Hmi=T/p(1)
And the attacking miner’s mining interval (minutes/blocks)
Ami=T/q(2)
How much time to extend the mainchain by z blocks, on average?
=z∗Hmi=z∗T/p(3)
How many blocks will attacker produce during honest miner’s time to mine z blocks?
Answering this question gives us the Poisson interval (lambda) of the attacker, expressed in the time expected for the honest nodes to produce a z block. It is the attacker’s block rate (inverse of 2) * the time available (3) or:
lambdaAttacker=q/T∗z∗T/p=zq/p(4)
Let us propose the attacker is tied at the AFD-1th block and must produce the AFDth block first. The probability is the sum of the probabilities that the attacker will produce any of 1 to infinity blocks in the time it takes the honest miners to produce z=1 blocks. Modelling mining as a Poisson process results in:
1−P(X=k successes=0,λ=zq/p)=k!λke−λ=1−e−zq/p=1−e−q/p(5)
Now let us propose that the attacker is tied at the AFD-2nd block and must win. This is the probability that the attacker produces 2 or more blocks (directly wins), or that the attacker produces 1 block times the probability of a win from that new position.
In general, if N blocks remain in the race, the probability of a win is the sum of the probability of producing 1,2,…N-1 blocks in one interval times the probability of winning from that new position, plus the probability that N or more blocks are discovered in this interval (which would be an automatic win):
The following equation is not quite correct, because it does not model the “head start” that the F chain gains if it mines more than 1 block within an M chain discovery interval. But it is presented here as a stepping stone.
W(N)=(i=1∑N−1P(X=i successes,q/p)W(N−i))+i=N∑∞P(X=i successes,q/p)
To fully express the model, we need to introduce variables denoting the main and fork lengths (Mlen and Flen):
W(N,Mlen,Flen)=⎩⎪⎪⎨⎪⎪⎧0 if Flen<Mlen,1 if Flen>=N, otherwise(i=1∑N−1−FlenP(X=i,q/p)W(N−i,Mlen+1,Flen+i))+i=N−Flen∑∞P(X=i,q/p)
This can be calculated and plotted for a variety of auto-finalization depths and attacker hash, resulting in the following graph (see Appendix 1 for jupyter code):
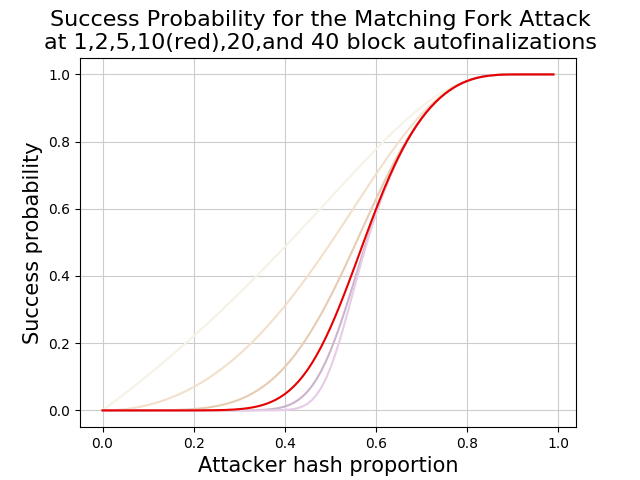
figure 1
Visually, this system is fairly robust against minority hash attackers at BCH’s 10 auto-finalization depth. Quantitatively, the likelihood of a successful attack by a 50% miner is only 25%. However, the situation changes rapidly above about 60% hash, with an attacker with 2/3rds of the hash power resulting in a 82% chance of success and a 3/4ths miner having an 94% likelihood of forcing a persistent fork.
These majority hash attacks are very relevant to a minority hash coin like BCH since a relatively small BTC miner can easily produce this hash power and direct it temporarily onto BCH. With an auto-finalization depth of 10, an attacker would have to redirect this hash power for about an hour to create a persistent fork.
Let us assume that hash power is readily available to be diverted to the attack. This is generally true for any “minor” blockchain – that is any chain that shares its proof-of-work algorithm with another chain that consumes the majority of the available hash power, and is true for BCH which is the only chain that the author is aware of that uses auto-finalization and fork parking. Without this assumption there is an unquantifiable cost to fabricate, deploy and manage the additional hash power required to execute this attack.
In BCH, the cost to mount the attack is the cost of production of 10 blocks. At the time of this writing, if we assume miners are breaking even, this would be approximately 10∗6.25∗250 or 15000 USD. This author feels that this is a very small amount compared to the profits that might be gained by leveraged short positions in BCH and executing one or multiple fork attacks. Additionally, forcing a persistent fork on a minority of services then abandoning it, can be used to double spend as described earlier.
It is unclear how BCH would “heal” a persistent fork. If the attacker’s chain is chosen as the main chain, there would be no loss to the attacker, except as caused by BCH price declines and the miner’s forced holding of the mined 62.5 BCH for 100 blocks. If the attacker’s chain is not chosen, all blocks are orphaned, so the cost is $14000 USD.
A P1 failure results in the loss of between 1 and 9 orphan blocks or between $1000 and $14000 USD.
A P2/P4 failure may result in the loss of between $1000 and $14000 USD, or no loss if the attacker’s fork is chosen as the main chain.
A P3 failure results in no loss of money.
A majority hash attack is much more likely to fail early than it is to fail later (especially with parking), since the more blocks mined, the more the majority chain tends to pull ahead of the minority. This means that failed attacks are more likely to incur losses on the lower end of the specified ranges.
We can now consider how fork “parking” affects the main attack described in this paper; the “fork matching” attack. Recall that “parking” causes nodes to resist switching forks unless the other fork’s work exceeds the current one by a variable amount as described earlier.
Note that “parking” significantly relaxes the finish criteria. If our attacker is working on the last block of F (at the auto-finalization depth - 1), M must be over 2*(auto-finalization depth - 1) blocks ahead to trigger F nodes to move back to M. This relationship is true for prior blocks as well, to fork depth 2. Ignoring the first 2 blocks, the F chain can grow half as fast as the M chain and still succeed.
A fork depth of 1 is not relevant, since that is the initial fork block. Parking does not affect the depth 2 block since the excess work is half a block. However, once the fork depth is 3 or greater, parking requires at least one block of extra work. This means that an arrival order problem will be ignored.
If the next M block is presented first to F-following nodes, it will not cause a chain switch. If the next F block is presented first to M-following nodes, there will similarly be no switch!
Parking therefore significantly reduces the likelihood of timing problems.
Similarly to the way attack mistiming becomes more lenient due to chain parking, minor variations in the chain work due to ASERT retargeting difficulty in every block will be ignored.
A significant problem is that the F chain must to stay even with or be ahead of the M chain every time a M block is found. This is a significantly more strict requirement than, for example, that the F chain eventually be even with the M chain (as is needed for the classic double spend attack). Parking relaxes this requirement to some degree. By block 3, the F chain can fall 1 block behind. And by block M > 3 the F chain can fall M blocks behind without triggering a chain switch. The probability analysis was rerun with the BCH parking rules, yielding the following graph
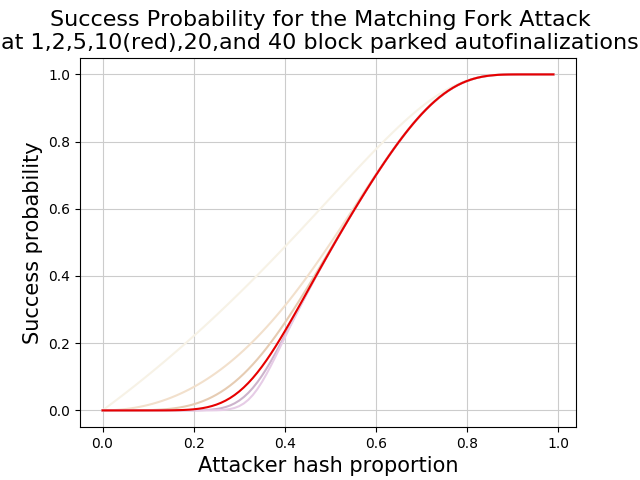
figure 2
Parking allows significantly less applied hash power to result in greater attack success probability, especially at lower hash levels. To repeat the data points presented earlier, 50% hash now has a 48% success rate (double), 66% an 83% success rate and 75% has a 94% success rate (about the same).
The follow graph plots the success probability for the traditional double spend and the fork matching attacks with and without 10 block finalization and BCH-algorithm parking. For double spend attacks, an embargo period of 10 blocks was chosen because it makes sense that exchanges would take advantage of the 10 block finalization.
Green is the standard double spend attack with a 10 block embargo period on a chain without finalization or parking. As first described in [1], since the attacker can theoretically mine forever, any attacker with > 50% of the hash power is guaranteed to succeed.
Blue is a “double spend attack”[f1] on a chain with finalization. Because of the finalization, the attack must succeed before the 10th main chain block is mined. This means that even if the attacker has majority hash power, it may get unlucky and be out-mined by the main chain. This is why the top of the curve smoothly approaches 1 as opposed to the Green line.
Yellow is a double spend attack on a chain with finalization and parking. As expected, it is significantly harder to succeed if the attacker must provide twice as much work as the main chain!
Red is a 10 block Fork Matching attack against a chain with finalization and parking. Interestingly, it has the highest success probability for minority hash attackers with about 20% to 35% of the hash. This is likely because parking’s extra required difficulty significantly helps the attack.
Orange is a 10 block Fork Matching attack against a chain with finalization only. As expected, it is harder for minority hash attackers than the red.
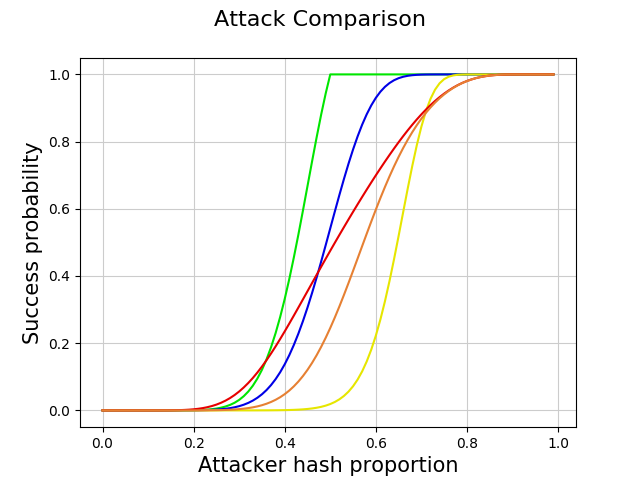
figure 3
Since a fork matching attack is effectively a persistent double spend attack, this last graph is concerning. In an attempt to eliminate double spend reorganizations, the ability to create persistent double spends was introduced. This is arguably worse, it will certainly be a lot harder to “clean up the mess” if such an attack is executed – likely requiring some centralized decision making.
More abstractly, the existence of theoretical results such as [5] and [6] that prove consensus impossible under certain constraints were deftly avoided by Satoshi because Bitcoin actually never achieves consensus. Instead it achieves a probability of consensus that increases as the statement’s depth in the chain increases. And in practice it eventually becomes economically infeasible for the statement to be changed.
The “consensus” achieved by Bitcoin Cash’s parking and auto-finalization technologies discourages intentional chain reorganization and completely prevents it beyond 10 blocks. But it is inconsistent with consensus theory and that strongly implies that these technologies are not innovations in consensus but rather a tradeoff. This tradeoff was neither identified or analyzed by the authors of these technologies, as far as I am aware. This paper furnishes that analysis and shows how these technologies can fail to achieve consensus and open avenues to execute the attacks they were intending to fix.
Instead of intentional chain reorganization, attackers can create intentional chain “deorganization”, achieving much the same outcome in terms of double spends or general mayhem. The question we may now want to ask is whether the risk of persistent consensus failure is worth the price of traditional double spend reorganization resistance?
[F1] The name “double spend attack” does not make much sense in this context since exchanges would use an embargo period greater than the finalization. So it would not be possible to execute an actual double spend (because the exchange would not release the goods before the reorganization). But this attack can reorganize the blockchain for other purposes, such as DoS.
[F2] Note that mining both the main chain and fork would also allow the attacker to deliver both M and F blocks directly to targets simultaneously, reducing the chance of propagation problems. It could also delay blocks it discovers on M.
[F3] Leading up to December 1, 2020, the BCHABC blockchain had been suffering a DOS attack from an anonymous miner that would mine mostly empty blocks and orphan blocks that did not pay 100% of the coinbase to ABC. In concert with ABC (as evidenced by explorer.bitcoinabc.org) a miner created a significant lower-work fork off of a 5 block chain that was created on Nov 30 (height 662687), but orphaned. On Dec 1, the BCHABC blockchain therefore had 2 significant consensus-compatible forks, which we can call BCHAA (most work) and BCHAB (less work). It is presumed that the ABC release’s networking code “preferred” BCHAB by initially connecting to BCHAB following nodes. During this time, network connectivity was inconsistent because connections to BCH would also consume connection slots. During 3 attempts to synchronize by 2 independent users, 2 nodes followed BCHAB and 1 followed BCHAA.
The following log shows how parking and finalization caused the lesser-work chain to be followed even though the node became aware of the greater-work chain (** indicates annotations):
2020-12-01T22:38:48Z UpdateTip: new best=00000000000000003cdfa4fb383f133cc22596eea61cb2bb4a2501cf20238f09 height=662686 version=0x20000000 log2_work=88.40692 tx=295435142 date='2020-11-30T18:30:46Z' progress=0.998904 cache=401.1MiB(2327112txo)
2020-12-01T22:38:48Z UpdateTip: new best=0000000000000000311ffccd67cba247a6db0a67fa2576174334fce036c48f84 height=662687 version=0x20000000 log2_work=88.40692 tx=295435154 date='2020-11-30T18:32:42Z' progress=0.998905 cache=401.1MiB(2327125txo)
2020-12-01T22:38:48Z UpdateTip: new best=000000000000000012b04da060e505a2c5917a8e9f2b329744880085a26ceda7 height=662688 version=0x20002000 log2_work=88.40692 tx=295435163 date='2020-11-30T18:36:57Z' progress=0.998908 cache=401.1MiB(2327136txo)
2020-12-01T22:38:48Z UpdateTip: new best=000000000000000024eaa803e4afb9db982dc2ad654a4d9576b838efb9740262 height=662689 version=0x20000000 log2_work=88.40692 tx=295435234 date='2020-11-30T18:42:34Z' progress=0.998912 cache=401.2MiB(2327346txo)
2020-12-01T22:38:48Z UpdateTip: new best=0000000000000000421f887e044db3791f520f8e8ef95fdb55c7116a8b843d89 height=662690 version=0x20000000 log2_work=88.406921 tx=295435237 date='2020-11-30T18:43:48Z' progress=0.998913 cache=401.2MiB(2327352txo)
2020-12-01T22:38:48Z UpdateTip: new best=00000000000000000b11d5c6599bb1ad4fa973355e508a7f25aef1b75aaefa7d height=662691 version=0x20c00000 log2_work=88.406921 tx=295435259 date='2020-11-30T18:51:16Z' progress=0.998917 cache=401.2MiB(2327382txo)
2020-12-01T22:38:48Z Pre-allocating up to position 0x700000 in rev01132.dat
2020-12-01T22:38:49Z UpdateTip: new best=0000000000000000212132b87c5d88d85796440bf7d74c5e50d770d87838784e height=662692 version=0x20000000 log2_work=88.406921 tx=295439836 date='2020-12-01T09:58:18Z' progress=0.999506 cache=401.3MiB(2328268txo)
2020-12-01T22:38:49Z Leaving InitialBlockDownload (latching to false)
2020-12-01T22:38:49Z UpdateTip: new best=00000000000000001f52576f7ebd17935a0591d8166ccc29b4776b3783f663bb height=662693 version=0x20800000 log2_work=88.406921 tx=295444566 date='2020-12-01T10:27:51Z' progress=0.999525 cache=401.3MiB(2328281txo)
2020-12-01T22:38:49Z UpdateTip: new best=00000000000000003574991e117505e6e35fa539d5923a29beff6531edb0f9c3 height=662694 version=0x2000e000 log2_work=88.406921 tx=295449299 date='2020-12-01T14:48:52Z' progress=0.999695 cache=401.3MiB(2328425txo)
2020-12-01T22:38:49Z UpdateTip: new best=00000000000000004ecde44b1f16bcd729bc7f3ae78e3448f44615c1729bdbf8 height=662695 version=0x20000000 log2_work=88.406921 tx=295454026 date='2020-12-01T15:05:26Z' progress=0.999705 cache=401.3MiB(2328441txo)
2020-12-01T22:38:49Z UpdateTip: new best=0000000000000000572b776c430b6228cb7cc8f5bee4df0132fa2ddd6a3bd025 height=662696 version=0x20000000 log2_work=88.406922 tx=295458755 date='2020-12-01T15:28:58Z' progress=0.999721 cache=401.3MiB(2328450txo)
2020-12-01T22:38:49Z UpdateTip: new best=000000000000000036f7e43405e0ce74bbca586eec7b45cb03201514b70ea61a height=662697 version=0x20c00000 log2_work=88.406922 tx=295463484 date='2020-12-01T15:45:29Z' progress=0.999731 cache=401.3MiB(2328461txo)
2020-12-01T22:38:49Z UpdateTip: new best=00000000000000002028199ed3fc89ce05be464b8aa3454c7977b06cece3d663 height=662698 version=0x20400000 log2_work=88.406922 tx=295468217 date='2020-12-01T16:12:57Z' progress=0.999749 cache=401.3MiB(2328478txo)
2020-12-01T22:38:49Z Pre-allocating up to position 0x800000 in rev01132.dat
2020-12-01T22:38:49Z UpdateTip: new best=000000000000000057dab39787431f06f01db7aacb33f22ac56775b160ae3848 height=662699 version=0x20000000 log2_work=88.406922 tx=295472946 date='2020-12-01T16:20:20Z' progress=0.999754 cache=401.3MiB(2328485txo)
2020-12-01T22:38:50Z UpdateTip: new best=000000000000000034d6eb357da13820d8cdbbd6a1b4b8044aee93ba9b293c77 height=662700 version=0x20000000 log2_work=88.406922 tx=295477674 date='2020-12-01T16:30:24Z' progress=0.999761 cache=401.3MiB(2328491txo)
2020-12-01T22:38:50Z UpdateTip: new best=00000000000000001d0653aa36ed906093b4039a4cc432757cab9127491f6f33 height=662701 version=0x20000000 log2_work=88.406922 tx=295482401 date='2020-12-01T16:31:13Z' progress=0.999761 cache=401.3MiB(2328495txo)
2020-12-01T22:38:50Z UpdateTip: new best=000000000000000035e71a8234c5a9384a83b3ac8f111393ec07ee5cd8d9d88c height=662702 version=0x20800000 log2_work=88.406923 tx=295487127 date='2020-12-01T16:40:42Z' progress=0.999767 cache=401.3MiB(2328497txo)
2020-12-01T22:38:50Z UpdateTip: new best=00000000000000003c75f89e752bc18c62bcc89823680276f216217c40343693 height=662703 version=0x20c00000 log2_work=88.406923 tx=295491859 date='2020-12-01T16:52:06Z' progress=0.999775 cache=401.3MiB(2328507txo)
2020-12-01T22:38:50Z UpdateTip: new best=000000000000000030d7c51fd01e65fcb64d5ecfb8a17dd115f2a8c4c1991499 height=662704 version=0x20000000 log2_work=88.406923 tx=295496591 date='2020-12-01T17:14:29Z' progress=0.999789 cache=401.3MiB(2328517txo)
2020-12-01T22:38:50Z UpdateTip: new best=00000000000000004fc834b1150d2b690b50530d59d80a61c9909e54934d56a5 height=662705 version=0x20000000 log2_work=88.406923 tx=295501317 date='2020-12-01T17:23:12Z' progress=0.999795 cache=401.3MiB(2328524txo)
2020-12-01T22:38:51Z UpdateTip: new best=000000000000000055e97a5a605a05ad729f366f4c8c036737b2cc17cd09f82f height=662706 version=0x3fff0000 log2_work=88.406923 tx=295506047 date='2020-12-01T17:35:34Z' progress=0.999803 cache=401.3MiB(2328542txo)
** this 662,687 in the largest POW fork chain **
2020-12-01T22:38:51Z Park block 00000000000000000709b858a6a0c8610e604e77072ef4407763afb0780ce712 as it would cause a deep reorg.
2020-12-01T22:38:51Z UpdateTip: new best=000000000000000006736ee57bcd3a2e45a4230d5923cb69e5e1e855a82508c9 height=662707 version=0x20000000 log2_work=88.406923 tx=295510774 date='2020-12-01T17:38:35Z' progress=0.999805 cache=401.3MiB(2328546txo)
2020-12-01T22:38:51Z UpdateTip: new best=0000000000000000229363232760bc77d9879c37d57646df5f6a3e2f35a987f2 height=662708 version=0x20000000 log2_work=88.406924 tx=295515500 date='2020-12-01T17:40:28Z' progress=0.999806 cache=401.3MiB(2328548txo)
2020-12-01T22:38:51Z Park block 00000000000000002cf08a4a14920aa0930b46c4e9092533adf570e7250db2b0 as it would cause a deep reorg.
2020-12-01T22:38:51Z UpdateTip: new best=00000000000000001322fddd281205d82fdfe459a992af6ab4cf87dad3d69338 height=662709 version=0x20400000 log2_work=88.406924 tx=295520223 date='2020-12-01T17:45:40Z' progress=0.999810 cache=401.3MiB(2328570txo)
2020-12-01T22:38:51Z UpdateTip: new best=000000000000000046b8dc899d847732f6548b6692ae28c6a94aeb4dffdb3a56 height=662710 version=0x20000000 log2_work=88.406924 tx=295524950 date='2020-12-01T17:53:49Z' progress=0.999815 cache=401.3MiB(2328573txo)
2020-12-01T22:38:51Z Park block 00000000000000004262b9f56c93d72a6f8e221f08c252e035aab5331f671f0a as it would cause a deep reorg.
2020-12-01T22:38:51Z UpdateTip: new best=00000000000000003ea89a75da1da763806264ca42d39f6e96f0dbf6cae8792f height=662711 version=0x20000000 log2_work=88.406924 tx=295529677 date='2020-12-01T17:56:02Z' progress=0.999816 cache=401.3MiB(2328578txo)
2020-12-01T22:38:51Z UpdateTip: new best=0000000000000000429e448460c0ee6800db0012f856d8082a639900617abc39 height=662712 version=0x20800000 log2_work=88.406924 tx=295534412 date='2020-12-01T18:30:21Z' progress=0.999839 cache=401.3MiB(2328614txo)
2020-12-01T22:38:51Z Park block 00000000000000003abc448d72e69babb9a13659aa14df995b13e76ff5b97612 as it would cause a deep reorg.
2020-12-01T22:38:52Z UpdateTip: new best=000000000000000047d42e0dc3b3431ef874c7ed68379762f77815fd8ecbac37 height=662713 version=0x20000000 log2_work=88.406924 tx=295539139 date='2020-12-01T18:32:35Z' progress=0.999840 cache=401.3MiB(2328616txo)
2020-12-01T22:38:52Z Pre-allocating up to position 0x900000 in rev01132.dat
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000000bcaf061b6acae7f2ba5126dbfbcee57fc47bc231c0ef679 height=662714 version=0x20000000 log2_work=88.406925 tx=295543865 date='2020-12-01T18:33:00Z' progress=0.999840 cache=401.3MiB(2328618txo)
2020-12-01T22:38:52Z Park block 00000000000000003fcb4ad579e937c831d6f39610bcc6714bed13de8392c7b4 as it would cause a deep reorg.
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000000261419163b30ef83854739da348b96d59156b788d1916fc height=662715 version=0x27d4e000 log2_work=88.406925 tx=295548595 date='2020-12-01T18:48:32Z' progress=0.999850 cache=401.3MiB(2328628txo)
2020-12-01T22:38:52Z UpdateTip: new best=000000000000000024b1b59b7d065b6e1a651d57b979ce6a7d0953045b5ca809 height=662716 version=0x20000000 log2_work=88.406925 tx=295552433 date='2020-12-01T19:15:29Z' progress=0.999868 cache=401.8MiB(2332504txo)
2020-12-01T22:38:52Z Park block 00000000000000003bdaacb7ec7f86049f2b4e0dc24031c8980daacb06bfdc8f as it would cause a deep reorg.
2020-12-01T22:38:52Z UpdateTip: new best=000000000000000037733987b917fa31d6a29d98f7b7c0552dd29edab05b0657 height=662717 version=0x20000000 log2_work=88.406925 tx=295552481 date='2020-12-01T19:36:34Z' progress=0.999882 cache=401.8MiB(2332521txo)
2020-12-01T22:38:52Z UpdateTip: new best=000000000000000038fd2290e132e392567448355b66981d053e9331823edb5a height=662718 version=0x20800000 log2_work=88.406925 tx=295552486 date='2020-12-01T19:37:30Z' progress=0.999882 cache=401.8MiB(2332728txo)
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000000fd22489326d22fa4bef1c29714cc24d9fc24e58b0d1370d height=662719 version=0x20000000 log2_work=88.406925 tx=295552520 date='2020-12-01T19:50:41Z' progress=0.999891 cache=401.8MiB(2332764txo)
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000003f82accf9bba20407036a480a62bd12cf6dcfed717fb333d height=662720 version=0x20c00000 log2_work=88.406926 tx=295552527 date='2020-12-01T19:54:10Z' progress=0.999893 cache=401.8MiB(2332767txo)
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000001c2a71c0f432f3cc4a0f7b98378bfc46d0ca176533e2b6df height=662721 version=0x20000000 log2_work=88.406926 tx=295552544 date='2020-12-01T19:56:45Z' progress=0.999895 cache=401.8MiB(2332781txo)
2020-12-01T22:38:52Z UpdateTip: new best=000000000000000030587c87406ab2d87c665c33bb0787436d7ea3fa310107ba height=662722 version=0x20000000 log2_work=88.406926 tx=295552547 date='2020-12-01T19:57:18Z' progress=0.999895 cache=401.8MiB(2332783txo)
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000002e3e2f4ec86fd2c78ec158d1c3f80f01d581f34c2b8bc7f4 height=662723 version=0x20000000 log2_work=88.406926 tx=295552567 date='2020-12-01T20:04:22Z' progress=0.999900 cache=401.8MiB(2332790txo)
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000004c402051bb2c7e3b707a32a9ef46caf6b64880d61dd68e31 height=662724 version=0x20a00000 log2_work=88.406926 tx=295552582 date='2020-12-01T20:11:29Z' progress=0.999904 cache=401.8MiB(2332863txo)
2020-12-01T22:38:52Z UpdateTip: new best=000000000000000038f822ea0ff410dd46cbb34a15718b30d4fc64c447532dfa height=662725 version=0x20000000 log2_work=88.406926 tx=295552584 date='2020-12-01T20:11:47Z' progress=0.999904 cache=401.8MiB(2332865txo)
2020-12-01T22:38:52Z UpdateTip: new best=0000000000000000373e32c0e86c53cf67e52c87dd44ca163fe87e4a536a736d height=662726 version=0x21f9e000 log2_work=88.406927 tx=295552609 date='2020-12-01T20:21:58Z' progress=0.999911 cache=401.8MiB(2332884txo)
2020-12-01T22:38:52Z UpdateTip: new best=000000000000000036d4885b9c3d95fe40ecbcaf1e2d285fb9eb4ed218c28924 height=662727 version=0x20000000 log2_work=88.406927 tx=295552672 date='2020-12-01T20:36:45Z' progress=0.999921 cache=401.9MiB(2332963txo)
2020-12-01T22:38:52Z UpdateTip: new best=000000000000000055bff8ca0427cae84d216f2801bf1f339794f99e3159569d height=662728 version=0x20000000 log2_work=88.406927 tx=295552725 date='2020-12-01T20:51:56Z' progress=0.999931 cache=401.9MiB(2333046txo)
2020-12-01T22:38:52Z UpdateTip: new best=000000000000000039c070a969fc765f2031932d9d7c1f64a941d9a026615a1c height=662729 version=0x3665c000 log2_work=88.406927 tx=295552789 date='2020-12-01T21:15:24Z' progress=0.999946 cache=401.9MiB(2333144txo)
2020-12-01T22:38:52Z Park block 000000000000000021aa2bc72cafb2cb4b462820676f6f997ca770a3491f2d20 as it would cause a deep reorg.
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000005aed86b69eb9adc40b1e076007a840e3ce76f03d73fb3a56 height=662730 version=0x20c00000 log2_work=88.406927 tx=295552791 date='2020-12-01T21:15:46Z' progress=0.999946 cache=401.9MiB(2333146txo)
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000000f43113d74f426be53cc46ece2978d91e37e914abb5fc8e3 height=662731 version=0x20000000 log2_work=88.406927 tx=295552861 date='2020-12-01T21:47:53Z' progress=0.999967 cache=401.9MiB(2333208txo)
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000004dca285e690ce3182654f7afb006cc07757ef5f1fe6e32aa height=662732 version=0x20800000 log2_work=88.406928 tx=295552947 date='2020-12-01T22:26:30Z' progress=0.999992 cache=401.9MiB(2333297txo)
2020-12-01T22:38:52Z Park block 000000000000000038b752df8d0de6f6dd23f54a20a6d1f66d91c5143e6c7dbc as it would cause a deep reorg.
2020-12-01T22:38:52Z UpdateTip: new best=00000000000000001ea3a6be94733d6bca00b1bbbabc3b5d92ce4a09f140a3c8 height=662733 version=0x20000000 log2_work=88.406928 tx=295552950 date='2020-12-01T22:26:58Z' progress=0.999992 cache=401.9MiB(2333317txo)
2020-12-01T22:38:52Z Park block 00000000000000003d7cf73caa7a7b7c4327789e0fd6d77236857969fcd4f2c1 as it would cause a deep reorg.
2020-12-01T22:38:52Z Park block 000000000000000002f93d655cf8dff674091eee848fcd33e520b940cd6cb43c as it would cause a deep reorg.
2020-12-01T22:38:52Z Park block 00000000000000002132e6597460cc9847daf8dad575afb1a3af343f15c6affb as it would cause a deep reorg.
2020-12-01T22:38:52Z Park block 0000000000000000052063889768c9edefe073733241444d57be155e5a005735 as it would cause a deep reorg.
2020-12-01T22:38:52Z Park block 00000000000000003aa7e890cf55d26aa81352270ab17f59c0a35c951c58282a as it would cause a deep reorg.
** Finalization causes the most POW chain to be invalidated **
2020-12-01T22:38:52Z Mark block 000000000000000003e7ea491122031d5508d60ccd78665fd8000efb37eb1e85 invalid because it forks prior to the finalization point 662723.
2020-12-01T22:38:52Z InvalidChainFound: invalid block=000000000000000003e7ea491122031d5508d60ccd78665fd8000efb37eb1e85 height=662858 log2_work=88.406959 date=2020-12-01T20:07:07Z
2020-12-01T22:38:52Z InvalidChainFound: current best=00000000000000001ea3a6be94733d6bca00b1bbbabc3b5d92ce4a09f140a3c8 height=662733 log2_work=88.406928 date=2020-12-01T22:26:58Z
** Finalization invalidation prevents the switch to the > POW chain during synchronization **
2020-12-01T22:38:52Z Considered switching to better tip 000000000000000003e7ea491122031d5508d60ccd78665fd8000efb37eb1e85 but that chain contains an invalid block.
2020-12-01T22:38:52Z CheckForkWarningConditions: Warning: Large fork found
forking the chain at height 662686 (00000000000000003cdfa4fb383f133cc22596eea61cb2bb4a2501cf20238f09)
lasting to height 662858 (000000000000000003e7ea491122031d5508d60ccd78665fd8000efb37eb1e85).
#!/usr/bin/python3
# Blockchain reorganization probability calculator
# Copyright 2020 G. Andrew Stone
# MIT Licensed (https://opensource.org/licenses/MIT)
# This file calculates and plots:
# 1. Satoshi (tie) double spend attack (chain reorganization) probabilities
# 2. Winning (1 extra block) double spend attack probabilities
# 3. Limited depth double spend attack probabilities
# 4. Chain matching attack probabilities verses finalization and/or parking blockchains
import math
def dspart(z,q,k):
p = 1.0 - q
lam = (z+1)*q/p
a = (lam**k)/(math.factorial(k)*(math.e**lam))
b = 1.0 - ((q/p)**(z+1-k))
return a*b
def doublespendAttack(z,q):
if (q>0.5):
return 1.0
sm = 0.0
for k in range(0,z+2): # +2 because range is not end inclusive, and it must be +1 because the attacker chain must exceed the honest
t = dspart(z,q,k)
sm += t
return 1.0 - sm
def doublespendAttackTie(z,q):
if (q>0.5):
return 1.0
sm = 0.0
for k in range(0,z+1): # +1 because range is not end inclusive
t = dspart(z,q,k)
sm += t
return 1.0 - sm
def poisson(success, lam):
return ( (lam**success)/(math.factorial(success)*(math.e**lam)) )
# The likelihood of poisson from success to infinity
def poissonNabove(success, lam):
acc = 0.0
for i in range(0,success): # goes from 0 to success-1 inclusive
acc += poisson(i,lam)
return 1-acc
calced2={}
def FinParkFork(attackerHash, Mlen, Flen, finalizationDepth, park):
# print(Flen, Mlen)
if (Flen >= finalizationDepth):
return 1.0
if park:
# cannot fall behind in fork depth 1 & 2
if (Mlen<3 and Flen<Mlen):
return 0.0
# can fall behind no more than 1 block in fork depth 3
elif (Mlen==3 and Flen<2):
return 0.0
# for other fork depths, attacker cannot fall behind more than double
elif (Flen*2 < Mlen):
return 0.0
elif (Flen < Mlen): # without parking, fork cannot ever fall behind
return 0.0
# Look in the cache for values we've already found
if (float(attackerHash),Mlen,Flen,finalizationDepth,park) in calced2:
return calced2[(float(attackerHash),Mlen,Flen,finalizationDepth,park)]
honestHash = 1-attackerHash
interval = attackerHash/honestHash
acc = 0.0
for i in range(0,finalizationDepth-Flen):
# Model the F chain finding i blocks while the M chain finds 1
acc += poisson(i,interval)*FinParkFork(attackerHash, Mlen+1, Flen+i, finalizationDepth, park)
# Model the F chain finding more than what it needs to win in this one interval
acc += poissonNabove(finalizationDepth-Flen, interval)
calced2[(float(attackerHash),Mlen,Flen,finalizationDepth,park)] = acc
return acc
calced3={}
def limitedDoubleSpendAttack(attackerHash, embargo, maxDepth, Mlen, Flen, park):
if park is True: # we are assuming the embargo is > 3 so the early parking rules do not matter
if Flen > Mlen*2 and Flen > embargo:
return 1.0
calcDepth = maxDepth*2
else:
if Flen > Mlen and Flen > embargo:
return 1.0
calcDepth = maxDepth
if (Mlen >= maxDepth): # Too late!
return 0.0
# Look in the cache for values we've already found
if (float(attackerHash),embargo,Mlen,Flen,maxDepth,park) in calced3:
return calced3[(float(attackerHash),embargo,Mlen,Flen,maxDepth,park)]
honestHash = 1-attackerHash
interval = attackerHash/honestHash
acc = 0.0
for i in range(0,calcDepth-Flen):
# Model the F chain finding i blocks while the M chain finds 1
acc += poisson(i,interval)*limitedDoubleSpendAttack(attackerHash, embargo, maxDepth, Mlen+1, Flen+i, park)
# Model the F chain finding more than what it needs to win in this one interval
acc += poissonNabove(calcDepth-Flen, interval)
calced3[(float(attackerHash),embargo,Mlen,Flen,maxDepth,park)] = acc
return acc
import numpy as np
import matplotlib.pyplot as pyplot
def plotFig1():
x = np.linspace(start=0.0, stop=0.99, num=100)
fig = pyplot.figure(1)
plt = fig.add_subplot()
plt.grid(color=(0.8,0.8,0.8))
plt.set_xlabel('Attacker hash proportion', fontsize=15)
plt.set_ylabel('Success probability', fontsize=15)
y2 = [ FinParkFork(i,0,0,1,False) for i in x]
plt.plot(x, y2, color=(.97,.95,0.9))
y2 = [ FinParkFork(i,0,0,2,False) for i in x]
plt.plot(x, y2, color=(.95,.88,0.8))
y1 = [ FinParkFork(i,0,0,5,False) for i in x]
plt.plot(x, y1, color=(.9,.8,.7))
y3 = [ FinParkFork(i,0,0,20,False) for i in x]
plt.plot(x, y3, color=(.8,.7,.8))
y4 = [ FinParkFork(i,0,0,40,False) for i in x]
plt.plot(x, y4, color=(.9,.8,.9))
y = [ FinParkFork(i,0,0,10,False) for i in x]
plt.plot(x, y, color=(.9,0,0))
fig.suptitle("Success Probability for the Matching Fork Attack\nat 1,2,5,10(red),20,and 40 block autofinalizations", fontsize=16)
fig.show()
def plotFig2():
x = np.linspace(start=0.0, stop=0.99, num=100)
fig = pyplot.figure(2)
plt = fig.add_subplot()
plt.grid(color=(0.8,0.8,0.8))
plt.set_xlabel('Attacker hash proportion', fontsize=15)
plt.set_ylabel('Success probability', fontsize=15)
y2 = [ FinParkFork(i,0,0,1,True) for i in x]
plt.plot(x, y2, color=(.97,.95,0.9))
y2 = [ FinParkFork(i,0,0,2,True) for i in x]
plt.plot(x, y2, color=(.95,.88,0.8))
y1 = [ FinParkFork(i,0,0,5,True) for i in x]
plt.plot(x, y1, color=(.9,.8,.7))
y3 = [ FinParkFork(i,0,0,20,True) for i in x]
plt.plot(x, y3, color=(.8,.7,.8))
y4 = [ FinParkFork(i,0,0,40,True) for i in x]
plt.plot(x, y4, color=(.9,.8,.9))
y = [ FinParkFork(i,0,0,10,True) for i in x]
plt.plot(x, y, color=(.9,0,0))
fig.suptitle("Success Probability for the Matching Fork Attack\nat 1,2,5,10(red),20,and 40 block parked autofinalizations", fontsize=16)
fig.show()
def plotFig3_differentAttacks():
x = np.linspace(start=0.0, stop=0.99, num=100)
fig = pyplot.figure(3)
plt = fig.add_subplot()
plt.grid(color=(0.8,0.8,0.8))
plt.set_xlabel('Attacker hash proportion', fontsize=15)
plt.set_ylabel('Success probability', fontsize=15)
# Green: standard doublespend attack, with a 10 block embargo period
z = [ doublespendAttack(10,i) for i in x]
plt.plot(x, z, color=(0,.9,0))
# Blue: 10 block doublespend attack with 10 block embargo period
embargo = 10
ldsa = [ limitedDoubleSpendAttack(i, embargo, 10, 0, 0, False) for i in x]
plt.plot(x, ldsa, color=(0,0,.9))
# Yellow: 10 block DS with 10 block embargo & parking
ldsa = [ limitedDoubleSpendAttack(i, embargo, 10, 0, 0, True) for i in x]
plt.plot(x, ldsa, color=(0.9,0.9,0))
# Red: 10 block Fork Matching attack against finalization & parking
y = [ FinParkFork(i,0,0,10,True) for i in x]
plt.plot(x, y, color=(.9,0,0))
# Orange: 10 block Fork Matching attack against finalization only
yy = [ FinParkFork(i,0,0,10, False) for i in x]
plt.plot(x, yy, color=(.9,.5,.2))
fig.suptitle("Attack Comparison", fontsize=16)
fig.show()
def Test():
print("F 50% at 10: ", FinParkFork(0.5,0,0,10,False))
print("F 66% at 10: ", FinParkFork(2.0/3.0,0,0,10,False))
print("F 75% at 10: ", FinParkFork(0.75,0,0,10,False))
print("PF 50% at 10: ", FinParkFork(0.5,0,0,10,True))
print("PF 66% at 10: ", FinParkFork(2.0/3.0,0,0,10,True))
print("PF 75% at 10: ", FinParkFork(0.75,0,0,10,True))
plotFig1()
plotFig2()
plotFig3_differentAttacks()
if __name__ == "__main__":
Test()
import code
code.interact()
[1]: Satoshi Nakamoto. The Bitcoin white paper
[2]: Parking as implemented in Bitcoin Cash Node in file validation.cpp function CBlockIndex *CChainState::FindMostWorkChain()
[4]: Ittay Eyal and Emin Gün Sirer. The Majority is Not Enough: Bitcoin Mining is Vulnerable
[5]: Fischer, Lynch, Patterson. Impossibility of Distributed Consensus with One Faulty
Process
[6]: Lamport, Shostak, Pease. The Byzantine General’s Problem
[7]: $5.6 Million Double Spent: ETC Team Finally Acknowledges the 51% Attack on Network
[8]: Coinbase: Ethereum Classic Double Spending Involved More Than $1.1 Million in Crypto